Application Note
Application Note #51: Inspired by the Oregonator
Bernd Ulmann
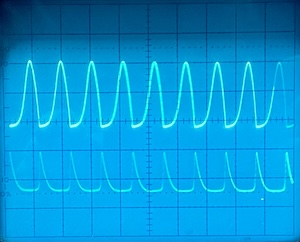
The Oregonator is a mathematical model for a certain class of autocatalytic chemical reactions. The name is a portmanteau of Oregon and oscillator as the system was developed by Richard J. Field and Richard M. Noyes at the University of Oregon.
About the author

Bernd Ulmann
Bernd Ulmann is a renowned expert in analog computing, with over 30 years of experience in IT, mathematics, and education. He is co-founder of anabrid GmbH, a company developing cutting-edge analog computing solutions and a professor at FOM University of Applied Sciences for Economics and Management in Frankfurt/Main. His expertise extends beyond academia and business. He is the curator of a unique Analog Computer Museum in Bad Schwalbach, Germany, which houses a world-class collection of analog computing devices. His passion for preserving and advancing analog technology has made him a prominent figure in the field.
More Publications

Application Note #2: The Lorenz-attractor
Bernd UlmannThis issue 2 of “Analog Computer Applications” deals with one of the most intriguing and well known chaotic attractors, the so-called Lorenz-attractor or -system. It was developed in 1963 by EdwardNorton Lorenz as a simplified model for atmospheric convection and first described in [Lorenz, 1963]. Although this seminal work was performed on a digital computer, a Royal McBee LGP-30, the Lorenz-attractor is ideally suited to be implemented on an analog computer.

Application Note #1: Rössler-attractor
Bernd UlmannAn electronic analog computer is ideally suited to study continuous-time dynamical systems of which those showing chaotic behavior are not only quite interesting but also yield aesthetically pleasing phase space plots. The particular system treated below was developed and studied in 1976 by Otto Rössler.

Application Note #3: The Chua-oscillator
Bernd UlmannAlthough unintended, it turned out that the first three issues of “Analog Computer Applications” are solely devoted to chaotic systems and their implementation on analog computers. This third issue deals with the so-called Chua-oscillator. This circuit was discovered in 1983 by Leon O. Chua and is a classic example of an electronic circuit exhibiting chaotic behavior.

Application Note #4: Airflow around an airfoil
Bernd UlmannThis application note deals with airflow around rotating cylinders and conformal mappings which transform the cross section of such a cylinder into a special type of airfoil.

Application Note #5: High-speed Bouncing Ball
Bernd UlmannThis application note describes the simulation of a ball bouncing in a box. Using high-speed integration, a flicker-free oscilloscope display of the ball’s path can be easily obtained.
Application Note #6: Zombie Apocalypse Now
Bernd UlmannHow could one not like zombie movies? It was about time that someone, Robert Smith? and his collaborators, shed some light on zombie attacks from a mathematical point of view.

Application Note #8: Nonlinear chaos
Bernd UlmannAn interesting chaotic system based on an absolute value function.

Application Note #7: Damped pendulum with external forcing function
Bernd UlmannA damped pendulum subjected to an external (harmonic) excitation function e(t) exhibits chaotic behavior and can be easily simulated on an analog computer as the following application note shows.
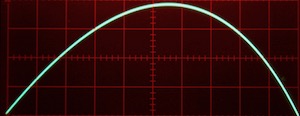
Application Note #9: Ballistic trajectory
Bernd UlmannThe following example computes the two-dimensional ballistic trajectory
of a projectile fired from a cannon, taking the velocity dependent drag
slowing the projectile down into account.
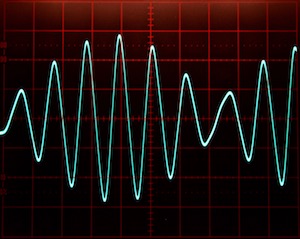
Application Note #10: Mathieu’s equation
Bernd UlmannThis application note deals with the well-known Mathieu equation, a linear homogenous second order di↵erential equation with many applications (it can be used to described the vibrations in an elliptic drum, or the behaviour of an inverted pendulum and many more).

Application Note #11: Celestial mechanics: Three-body problem
Bernd UlmannSimulating (or determining) the movement of three (celestial) bodies with given parameters (masses, gravitational constant, initial conditions for the bodies’ coordinates and velocities) is known as the three-body problem.
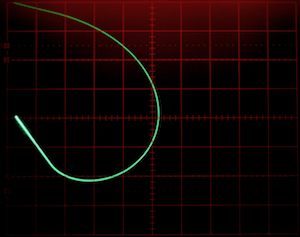
Application Note #12: Charged particle in a magnetic field
Bernd UlmannIn the following, the path of a charged particle flying through a magnetic field is simulated by an analog computer..

Application Note #13: Trajectory optimization on a hybrid computer
Bernd UlmannThe idea of coupling an analog computer with a digital computer, thus creating a so-called hybrid computer, is by no means new, but nevertheless intriguing as it makes it possible to combine the best of both worlds of computing. The first hybrid computers were built in the mid-1950s to aid in aerospace research.

Application Note #14: Rutherford-scattering
Bernd UlmannIn the early 20th century, Ernest Rutherford performed a seminal experiment in which he bombarded a thin gold foil with a-particles. He observed that the vast majority of these particles, actually Helium nuclei, just went through the gold foil without being deflected or absorbed. Nevertheless, some of these particles were deflected through large angles, with even fewer a-particles being reflected by the gold foil, a phenomenon called Rutherford-scattering. This led to the planetary Rutherford model of the atom which became the basis of the Bohr model.

Application Note #15: Elegant Chaos
Bernd UlmannOne of the most intriguing books on chaotic systems is [Sprott 2010] which is a true treasure trove for everybody fascinated by these mathematical objects. In the following, we will implement two of these systems on an analog computer.

Application Note #16: Yet another Lorenz system
Bernd UlmannRecently, I stumbled over Peter McNair’s gerat blog Analog Ontology, where he describes – among many other highly interesting things – his implementation of a rather unknown attractor devised by Edward N. Lorenz. In 1984 Lorenz published a paper titled Irregularity: a fundamental property of the atmosphere where he describes a system of three coupled differential equations.

Application Note #17: The Aizawa attractor
Bernd UlmannThis application note implements one of the most beautiful chaotic attractors, the so-called Aizawa attractor.

Application Note #19: A simple spacecraft simulation
Bernd UlmannThis application note describes a pretty simple spacecraft simulation that allows a person to control a spacecraft in empty space by firing rotational and translational thrusters using a joystick with an adapter like that described in the previous analog computer application note (#18).

Application Note #18: A simple joystick adapter
Bernd UlmannIt cannot be said often enough: “An analog computer is thing of beauty and a joy forever.” And an analog computer is a wonderful toy for those mathematically inclined, but what would be a toy without a joystick? This short application note shows a simple adapter circuit which allows the use of a two-channel analog joystick as commonly used in model building with an analog computer.

Application Note #20: Simulating an inverted pendulum
Berrnd UlmannThis application note describes the simulation of an inverted pendulum, i. e. a pendulum that has its mass above its pivot point which is mounted on a cart capable of moving along the x-axis as shown in figure 1. The aim is to keep this pendulum in its upright position by controlling a force F acting on the cart in order to move it from left to right and vice versa.

Application Note #21: Simulating a double pendulum
Bernd UlmannThis application note describes the simulation of a double pendulum on an analog computer.
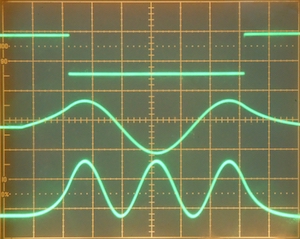
Application Note #22: Solving the Schr¨odinger equation
Bernd UlmannThis application note describes how to solve the time independent Schrödinger equation for a nonrelativistic particle in one dimension on an analog computer.
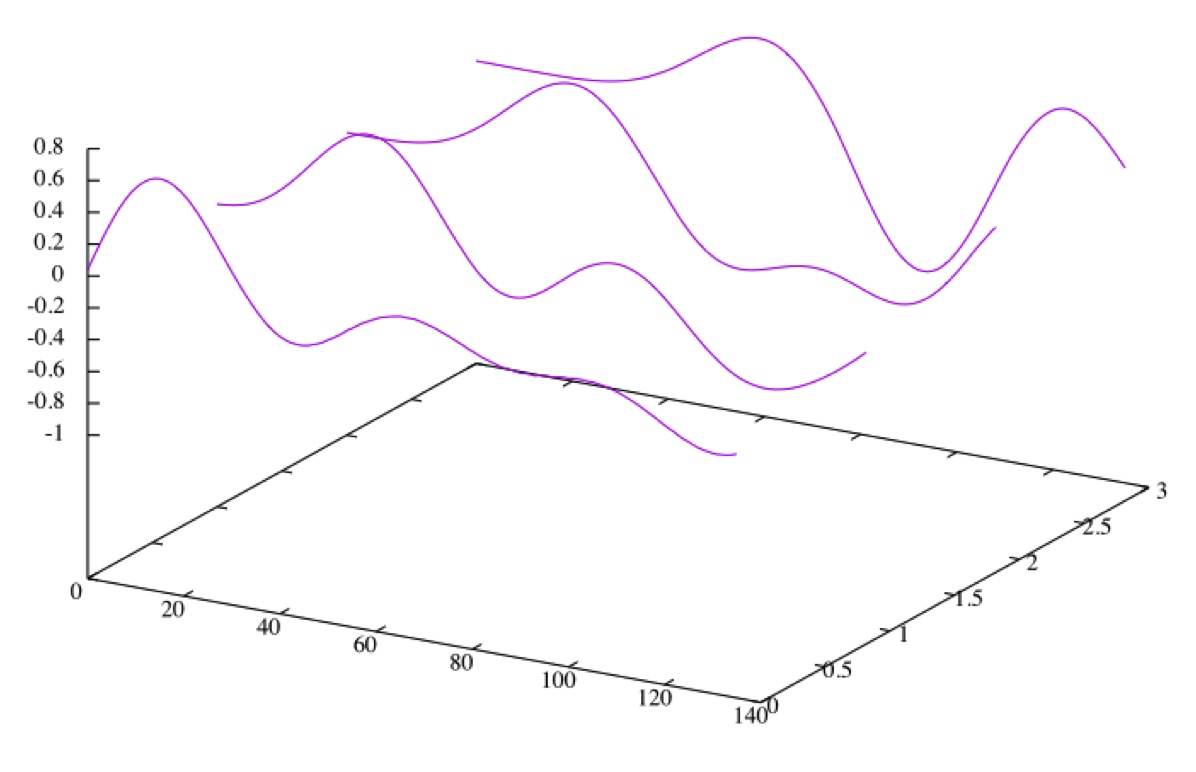
Application Note #23: Solving PDEs on an analog computer
Bernd UlmannThis application note shows a simple and straightforward way to solve partial di↵erential equations (PDE s for short) on an analog/hybrid computer. It also shows how to use the Analog Paradigm hybrid controller to control the analog computer, gather data and generate a plot of the results.
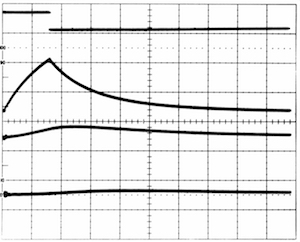
Application Note #24: Solving the two-dimensional heat-equation
Bernd UlmannThe aim of this application note is to solve the two-dimensional heat equation on an analog computer.
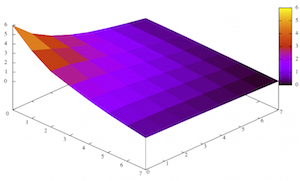
Application Note #25: A passive network for solving the two-dimensional heat equation
Bernd UlmannThe aim of this application note is to show how the two-dimensional heat transfer equation can be solved using a passive resistor-capacitor (RC) network.

Application Note #26: Simulating the flight of a glider
Bernd UlmannIn the early years of the 20th century, the English engineer and polymath Frederick William Lanchester1 discovered the phenomenon of phugoid oscillation, which describes the motion of an aircraft pitching up and climbing only to pitch down and descend.2 The angle of attack, AOA, of the airplane is next to constant during motion while it experiences an oscillatory exchange of airspeed and altitude.

Application Note #27: Making music
Bernd UlmannAn analog computer is not too di↵erent from a synthesizer, so the idea of making music with and on an analog computer is pretty obvious. This application note describes a pretty simple computer setup that turns an analog computer into a monophonic synthesizer controlled by a keyboard with voltage outputs for gate and pitch.
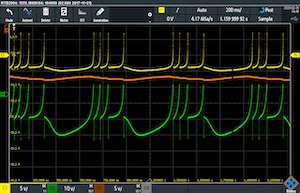
Application Note #28: The Hindmarsh-Rose-model of neuronal bursting
Bernd UlmannBeginning in the early 20th century, the behaviour of neurons has been described by increasingly realistic mathematical models. The very first of these models is called integrate-and-fire and is due to Lous Lapicque who developed it in 1907. [... A much more interesting model is due to Hindmarsh and Rose and consists of three coupled differential equations]
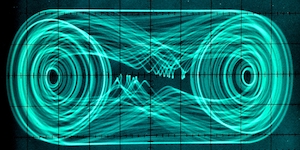
Application Note #29: The Duffing Oscillator
Bernd UlmannA Duffing equation describes any oscillator featuring a cubic stiffness term, i. e. a nonlinear elasiticity. It is named after Georg Wilhelm Christian Caspar Duffing (1861 – 1944), a German engineer and inventor who wrote a seminal work on forced oscillations in 1918.
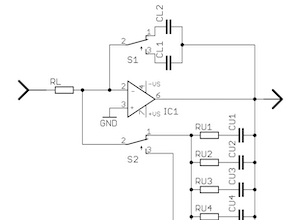
Application Note #30: Neutron kinetics
Bernd UlmannThis application note deals with a simple implementation of neutron kinetics for nuclear reactors fuelled with U235 or Pu239 respectively. It will be part of a little series of application notes culminating in the simulation of a nuclear power plant on an analog computer.

Application Note #31: Sprott SQM model
Bernd UlmannThis application note implements the SQM model (cf. [Sprott(2016), pp. 68ff.]), an example of a simple three-dimensional chaotic flow with a quadratic nonlinearity.

Application Note #32: The exponentially-mapped-past approach
Bernd UlmannIt is often desirable to compute something like an arithmetic mean. [...]The basic idea is to introduce a weighting function that ensures that recent values influence the result more strongly than values in the past. The following equation demonstrates this technique with the integral running from the most distant past −∞ to 0 (=“now”)

Application Note #33: The Euler spiral
Bernd UlmannThe first example in the beautiful book [Havil(2019), pp. 1 ff.] is the Euler spiral, which is a clothoid, i. e. a curve with a curvature depending linearly on the arc length. Clothoids play a significant role in road and railway track construction. Imagine driving along a straight road, approaching a curve. If the straight part of the road was directly connected to an arc of a circle forming the curve, one would have to switch from a steering angle of zero to a non-zero steering angle instantaneously, which is impracticable even at rather low speeds. Therefore, a safe curve in a road has a curvature that starts at zero, rises to a maximum and then falls back to zero again when the next straight segment of the road is entered. This can be done by using clothoids and many curves encountered on highways and railway tracks are based on this type of curve.
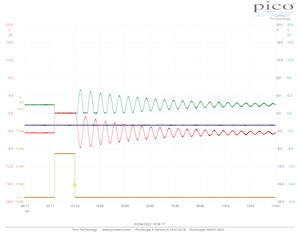
Application Note #34: Beyond the spring-mass-damper
Bernd UlmannThis Application Note has been written to give the reader some suggestions for extending the classic Spring-Mass-Damper model to a more complex real-world problem – bungee jumping!

Application Note #35: Generating Bessel functions
Bernd UlmannIn June 2022, fellow analog computer enthusiast Dr. Chris Giles sent me a classic exercise shown in figure 1. This exercise is the basis of this application note.
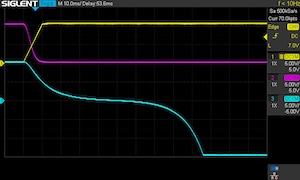
Application Note #36: Quantum Mechanical Two-Body Problem with Gaussian potential
Bernd UlmannThis application note is inspired by the work described in [Thies et al. 2022]. In this paper the authors develop a numerical method to calculate binding energies of a quantum mechanical three-body system efficiently. This three-body system is composed of two heavy and one light particle. In figure 1 the system is displayed with its two-body (heavy/light) subsystems marked by dashed ellipses. The routine to calculate binding energies for the three-body system first solves the two-body subsystem. This application note aims to reproduce the findings in [Thies et al. 2022] for the two-body systems using an analog computer.

Application Note #37: Displaying polynomials
Bernd UlmannAn analog computer is a wonderful educational tool due to its unmatched high degree of interactivity. Running in repetitive mode of operation it is possible to immediately see the effects of changing parameters in a program on an oscilloscope screen. This application note describes a simple analog computer program to display a polynomial.
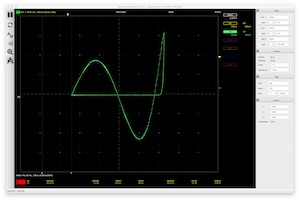
Application Not#38: Solving Legendre’s differential equation
Bernd UlmannSolving Legendre’s differential equation
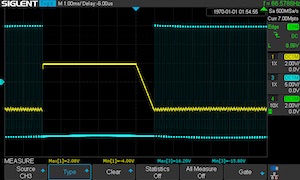
Application Note #39: Finding roots of nonlinear equations
Bernd UlmannThis application note draws inspiration from the work of Huang et al.. The continuous Newton method is a powerful numerical algorithm for solving nonlinear equations that has been gaining popularity due to its efficiency and robustness. However, its implementation on digital computers can be computationally expensive, especially for problems with a large number of variables.

Application Note #40: The Brusselator
Bernd UlmannThe Brusselator is set of two coupled differential equations describing the following autocatalytic chemical reaction.

Application Note #41: Experiments with Hindmarsh-Rose neurons
Bernd UlmannThe Hindmarsh-Rose model of neural bursting was already topic of application note #28. This application note extends such neurons with excitatory and inhibitory inputs allowing to couple several neurons to obtain more complex behavior.

Application Note #42: Generating a Gaussian function
Bernd UlmannGenerating a Gaussian function

Application Note #43: A chaotic Sprott system
Bernd UlmannA dark and rainy Sunday – what could be better than staying at home where it is warm and cosy and playing with an analog computer like THE ANALOG THING. This application shows the implementation of a simple chaotic Sprott system.
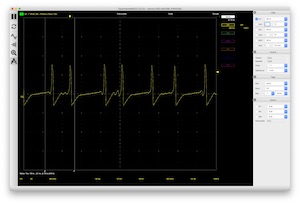
Application Note #44: Three Time-Scale System
Bernd UlmannMequations (DEQs) involving (vastly) different time scales. Typical examples are ample in areas such as biochemistry, chaotic systems, oscillators, neurophysiology, chemical reaction kinetics, etc.
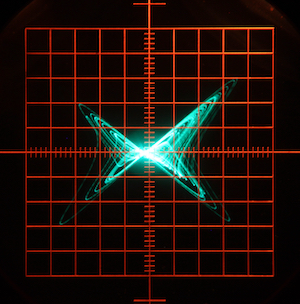
Application Note #45: A four-wing attractor
Bernd UlmannThis application note describes a rather beautiful “four-wing attractor”, which is due to [Wang et al. 2009].
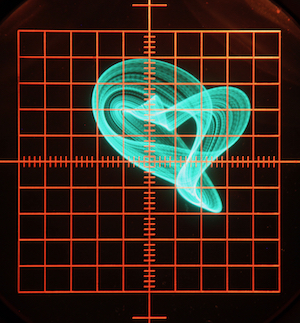
Application note #46: Four times chaos
Bernd UlannAfter quite some hiatus, the analog computer application notes are back with more chaotic systems, a topic I am quite fond of. :-) Four such systems are described in the following. The first three systems require three multipliers and thus need THE ANALOG THINGs while the last system only needs one multiplier and runs on a single THE ANALOG THING.

Application Note #47: Mathieu’s equation revisited
Bernd UlmannAs simple as it looks at first glance, Mathieus’s equation exhibits highly interesting behaviour under control of its two parameters a and q. It was already the subject of an application note1 dating back to 2017. This application note itself was mostly based on an even more classic one by EAI, see [EAI 7.4.4a]. On page 4 in this source a stability diagram is shown, which sparked the idea of creating such a map using a hybrid computer setup. It should be noted that the definitive source on the overall topic of Mathieu’s equation and Mathieu functions is [McLachlan 1947], which is highly recommended.
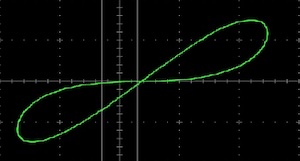
Application Note #48: A simple memristor model
Bernd UlmannIn 1971, Leon O. Chua proposed a novel passive electronic circuit element1 as the fourth basic circuit element complementing the resistor, inductor, and capacitor. Back then it was a purely theoretical concept, which only became a reality in recent years with several companies working in that field.

Application Note #49: Fun with sinc(t)
Bernd UlmannThis application note shows two approaches for generating sinc(x) for x>0 (and not too large). In both cases x is replaced by the machine time t, which is generated by integrating over a (small) constant.
Application Note #50: Stochastic DEQs and hybrid computing
Bernd UlmannThe goal of this application note is not to solve this particular SDE but to use it to demonstrate how a hybrid computer, i. e., an analog computer coupled with a digital computer, can be employed to treat problems like this in general. Accordingly, the Wiener process is implemented by an electronic noise generator without caring too much about its actual output signal’s stochastic properties. In the same manner the parameters λ and σ were chosen arbitrarily so that no overloads occured at the end of the individual computing runs.

Application Note #52: The Chen attractor
Bernd UlmannThis short application note deals with the Chen attractor which is described in detail in [Augustova et al. 2013] and [Jasim et al. 2011].

Application Note #53: Thomas’ Cyclically Symmetric Attractors
Bernd UlmannThomas’ Cyclically Symmetric Attractors

Application Note #54: The Li system
Bernd UlmannIn [Letellier et al. 2007] a Lorenz-like chaotic system, the Li system, is analysed in detail. This system is implemented on two THE ANALOG THINGs in this application note with a special emphasis on scaling which is a bit tricky in this particular case.

